Address Calculation in Single and Double Dimension Array - ISC Computer Science

-

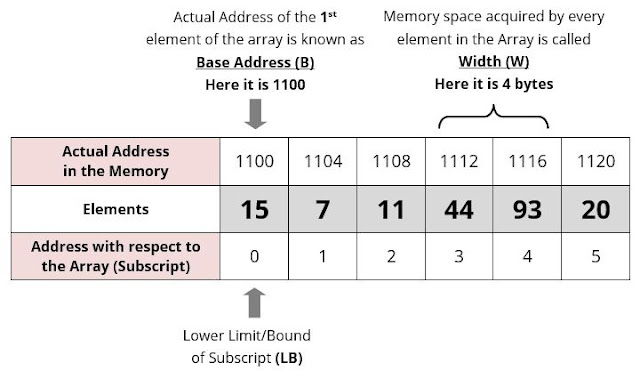
Address Calculation in single (one) Dimension Array:




Array of an element of an array say “A[ I ]” is calculated using the following formula:
Address of A [ I ] = B + W * ( I – LB )
Where,
B = Base address
W = Storage Size of one element stored in the array (in byte)
I = Subscript of element whose address is to be found
LB = Lower limit / Lower Bound of subscript, if not specified assume 0 (zero)
Example:
Given the base address of an array B[1300…..1900] as 1020 and size of each element is 2 bytes in the memory. Find the address of B[1700].
Solution:
The given values are: B = 1020, LB = 1300, W = 2, I = 1700
Address of A [ I ] = B + W * ( I – LB )
= 1020 + 2 * (1700 – 1300)
= 1020 + 2 * 400
= 1020 + 800
= 1820 [Ans]


Address Calculation in Double (Two) Dimensional Array:
While storing the elements of a 2-D array in memory, these are allocated contiguous memory locations. Therefore, a 2-D array must be linearized so as to enable their storage. There are two alternatives to achieve linearization: Row-Major and Column-Major.


Address of an element of any array say “A[ I ][ J ]” is calculated in two forms as given:
(1) Row Major System (2) Column Major System
Row Major System:
The address of a location in Row Major System is calculated using the following formula:
Address of A [ I ][ J ] = B + W * [ N * ( I – Lr ) + ( J – Lc ) ]
Column Major System:
The address of a location in Column Major System is calculated using the following formula:
Address of A [ I ][ J ] Column Major Wise = B + W * [( I – Lr ) + M * ( J – Lc )]
Where,
B = Base address
I = Row subscript of element whose address is to be found
J = Column subscript of element whose address is to be found
W = Storage Size of one element stored in the array (in byte)
Lr = Lower limit of row/start row index of matrix, if not given assume 0 (zero)
Lc = Lower limit of column/start column index of matrix, if not given assume 0 (zero)
M = Number of row of the given matrix
N = Number of column of the given matrix
Important : Usually number of rows and columns of a matrix are given ( like A[20][30] or A[40][60] ) but if it is given as A[Lr- – – – – Ur, Lc- – – – – Uc]. In this case number of rows and columns are calculated using the following methods:
Number of rows (M) will be calculated as = (Ur – Lr) + 1
Number of columns (N) will be calculated as = (Uc – Lc) + 1
And rest of the process will remain same as per requirement (Row Major Wise or Column Major Wise).
Examples:
Q 1. An array X [-15……….10, 15……………40] requires one byte of storage. If beginning location is 1500 determine the location of X [15][20].
Solution:
As you see here the number of rows and columns are not given in the question. So they are calculated as:
Number or rows say M = (Ur – Lr) + 1 = [10 – (- 15)] +1 = 26
Number or columns say N = (Uc – Lc) + 1 = [40 – 15)] +1 = 26
(i) Column Major Wise Calculation of above equation
The given values are: B = 1500, W = 1 byte, I = 15, J = 20, Lr = -15, Lc = 15, M = 26
Address of A [ I ][ J ] = B + W * [ ( I – Lr ) + M * ( J – Lc ) ]
= 1500 + 1 * [(15 – (-15)) + 26 * (20 – 15)] = 1500 + 1 * [30 + 26 * 5] = 1500 + 1 * [160] = 1660 [Ans]
(ii) Row Major Wise Calculation of above equation
The given values are: B = 1500, W = 1 byte, I = 15, J = 20, Lr = -15, Lc = 15, N = 26
Address of A [ I ][ J ] = B + W * [ N * ( I – Lr ) + ( J – Lc ) ]
= 1500 + 1* [26 * (15 – (-15))) + (20 – 15)] = 1500 + 1 * [26 * 30 + 5] = 1500 + 1 * [780 + 5] = 1500 + 785
= 2285 [Ans]


Comments

  1. Kingzz21 January 2019 at 02:58

    Doing a great job brother...!!! Keep Shining..!!

    ReplyDelete
  2. Neha kumari14 April 2021 at 02:16

    https://ziyyara.in/home-tuition/online-home-tuition-for-isc-board
    "Ziyyara’s ISC tutor offers one-to-one online home tuition for ISC Board students.They implement pedagogy teaching methods while delivering online tuition classes."
    Visit On:- gcse online tuition
    Phone no - +91-9654271931

    ReplyDelete
  3. Rudraksh Sharma1 January 2024 at 20:50

    Thank you for providing such an informative blog. Choose our online tuition for computer science, at Ziyyara. Our user-friendly online platform ensures seamless communication between you and your tutor, enabling personalized learning at your convenience. Don't let computer science overwhelm you anymore – enroll with Ziyyara today and unlock your full potential.
    Visit Ziyyara.com or contact us at +91 9654271931

    ReplyDelete

Post a Comment

Popular posts from this blog

ICSE Class 10 - Computer Application Important Program (15 Marks)

-
Program 1-  Define a class called Library with the following description: Instance variables/data members: Int acc_num – stores the accession number of the book String title – stores the title of the book stores the name of the author Member Methods: (i) void input() – To input and store the accession number, title and author. (ii)void compute – To accept the number of days late, calculate and display and fine charged at the rate of Rs.2 per day. (iii) void display() To display the details in the following format: Accession Number Title Author Write a main method to create an object of the class and call the above member methods. Solution -  public class Library {     int acc_num;     String title;     String author;     public void input() throws IOException {         BufferedReader br = new BufferedReader(new InputStreamReader(System.in));         System.out.print("Enter accession number: ");         acc_num = Integer.parseInt(br.readLine
Read more

ICSE Class 10 - Computer Application Important Questions & Answers (2 Marks)

-
02 (Two) Marks Questions  Question 1- Give one example each of a primitive data type and a composite data type. Ans.  Primitive Data Types – byte, short, int, long, float, double, char, boolean Composite Data Type – Class, Array, Interface Question 2- Give one point of difference between unary and binary operators.  Ans.  A unary operator requires a single operand whereas a binary operator requires two operands. Examples of Unary Operators – Increment ( ++ ) and Decrement ( — ) Operators Examples of Binary Operators – +, -, *, /, % Question 3- Differentiate between call by value or pass by value and call by reference or pass by reference. Ans.  In call by value, a copy of the data item is passed to the method which is called whereas in call by reference, a reference to the original data item is passed. No copy is made. Primitive types are passed by value whereas reference types are passed by reference. Question 4- Write a Java expression for (under root
Read more

COMPUTER SCIENCE PRACTICAL SOLVED QUESTIONS - ISC BOARD 2018

-
Image
QUESTION -1 A Goldbach number is a positive even integer that can be expressed as the sum of two odd primes. Note: All even integer numbers greater than 4 are Goldbach numbers. Example: 6 = 3 + 3 10 = 3 + 7 10 = 5 + 5 Hence, 6 has one odd prime pair 3 and 3. Similarly, 10 has two odd prime pairs, i.e. 3 and 7, 5 and 5. Write a program to accept an even integer ‘N’ where N > 9 and N < 50. Find all the odd prime pairs whose sum is equal to the number ‘N’. Test your program with the following data and some random data: Example 1: INPUT: N = 14 OUTPUT: PRIME PAIRS ARE: 3, 11 7, 7 Example 2: INPUT: N = 30 OUTPUT: PRIME PAIRS ARE 7, 23 11, 19 13, 17 Example 3: INPUT: N = 17 OUTPUT: INVALID INPUT. NUMBER IS ODD. Example 4: INPUT: N = 126 OUTPUT: INVALID INPUT. NUMBER OUT OF RANGE. import java.util.*; public class Goldbach {     boolean isPrime(int n)     {         if(n<=1)        //All numbers that are less than or equal to one are  non-pr
Read more

ICSE CLASS 10 COMPUTER APPLICATION - Chapter 1: Concept of Objects

-
1.   Give two examples of real-world objects. Also specify their characteristics and behaviour. Ans. Real Life Objects Example1: Object Name:    Pen Characteristics: Company made, Colour, Body Shape and Nip. Behaviour: 1)       Used for writing. 2)       Used for correction 3)       Used for drawing or sketching Example 2: Object Name:      Dog Characteristics: Name, Colour and Breed. Behaviour: 1)       Barking 2)       Wagging its tail 3)       Running speed 2.   What do you understand by state of an object? Explain with an example. Ans. State of an object refers to the condition in which an object is in. Thus the values/attributes of its characteristics is represented For example, a book is an object, which may be either in “open” or “closed” state, similarly a bulb may be in switched on or switched off state. 3.   How are objects implemented in Software? Ans. Every object in real life has certain charac
Read more

ISC Computer Science - Propositional Logic

-
Propositional Logic Logic  is a formal method of reasoning. A  proposition  is an elementary atomic sentence that may either be true or false but may take no other value. A  simple proposition  is one that does not contain any other proposition as a part. A  compound proposition  is one with two or more simple propositions as parts. An  operator  or  connective  joins simple propositions into compounds. Following are the various types of connectives: 1.     Disjunctive (OR) : It means at least one of the two arguments is true. OR is represented by + or ∨ . 2.     Conjunctive (AND) : It means that both the arguments are true. AND is represented by or & or ∧ . 3.     Conditional (Implication or If Then) : It means that if one argument is true then other argument is true. Implication is represented by ⇒ or → or ⊃ . 4.     Bi-conditional (Equivalence or If And Only If):  It means that either both arguments are true or both are false. Equivalence is represented
Read more

COMPUTER SCIENCE PRACTICAL SOLVED QUESTIONS - ISC BOARD 2016

-
Question 1: A  Circular Prime  is a prime number that remains prime under cyclic shifts of its digits. When the leftmost digit is removed and replaced at the end of the remaining string of digits, the generated number is still prime. The process is repeated until the original number is reached again. A number is said to be prime if it has only two factors I and itself. Example: 131 311 113 Hence, 131 is a circular prime. Test your program with the sample data and some random data: Example 1 INPUT : N = 197 OUTPUT: 197 971 719 197 IS A CIRCULAR PRIME Example 2 INPUT : N = 1193 OUTPUT: 1193 1931 9311 3119 1193 IS A CIRCULAR PRIME Example 3 INPUT : N = 29 OUTPUT: 29 92 29 IS NOT A CIRCULAR PRIME Programming Code: import java.util.*; class CircularPrime_Q1_ISC2016 {      boolean isPrime(int n) // Function for checking whether a number is prime or not      {          int c = 0;          for(int i = 1; i<=n; i++)         
Read more

ICSE CLASS 10 COMPUTER APPLICATION - Chapter 2: The Java Phenomenon

-
1.   What is the significance of WWW? Ans. WWW or World Wide Web allows a huge pool of information (as web pages) to shared by multiple users over a World Wide Network (Internet) and the introduction of Java makes the web pages dynamic and interactive in a secured manner. 2.   What is Browsing? Ans. Browsing over the internet allows surfing through the internet, thus enabling the users to see information in different pages and interact with it. 3.   Name two types of Java programs. 4.   Why is Java choice for the Web? Ans. The introduction of active web pages makes Java an attractive addition to the web page. When we click on a web page containing a Java applet, it is not that we just read it, listen to it, or watch it– we can interact with it. The dynamic, interactive content to the web was brought about by Java: So much so web applications made in Java runs as if it is a computer program installed in the local computer. 5.   What is Jav
Read more

Computer Science Paper 1 (Theory) - ISC 2018

-
Image
Computer Science Paper 1 (Theory) - ISC 2018 - Page-1 Computer Science Paper 1 (Theory) - ISC 2018 - Page-2 Computer Science Paper 1 (Theory) - ISC 2018 - Page-3 Computer Science Paper 1 (Theory) - ISC 2018 - Page-4 Computer Science Paper 1 (Theory) - ISC 2018  - Page-5 Computer Science Paper 1 (Theory) - ISC 2018 - Page-6 Computer Science Paper 1 (Theory) - ISC 2018 - Page-7 Computer Science Paper 1 (Theory) - ISC 2018 - Page-8 Computer Science Paper 1 (Theory) - ISC 2018 - Page-9
Read more

Important Programme in JAVA for Class 10 ICSE Board

-
Programme List 1-  Write a  program to print the first 15 numbers of the Pell series in JAVA Prgramming Language In mathematics, the Pell numbers are an infinite sequence of integers. The sequence of Pell numbers starts with 0 and 1, and then each Pell number is the sum of twice the previous Pell number and the Pell number before that.: thus, 70 is the companion to 29, and 70 = 2 × 29 + 12 = 58 + 12. The first few terms of the sequence are : 0, 1, 2, 5, 12, 29, 70, 169, 408, 985, 2378, 5741, 13860 2-  Write a programme to check whether a number is a MAGIC number or not?  
Read more